矩阵
1. 矩阵类型
引擎用于表示矩阵的类型有以下两种:
XMATRIX3 表示一个 3x3的矩阵,成员变量是3x3的二维浮点数数组。
$$ \begin{matrix} 11 & 12 & 13\ 21 & 22 & 23\ 31 & 32 & 33\ \end{matrix}
$$
XMATRIX4 表示一个 4x4的矩阵,成员变量是4x4的二维浮点数数组。
$$ \begin{matrix} 11 & 12 & 13 & 14\ 21 & 22 & 23 & 24\ 31 & 32 & 33 & 34\ 41 & 42 & 43 & 44 \end{matrix}
$$
2. 矩阵的意义
一个标准的4x4矩阵可以表达线性变换一系列的平移、旋转、缩放操作。
举个例子,我们目前有一个小明Actor,我们想控制这个小明往前方走5米。那么很简单,我们可以很简单地表示为:
---@type XVECTOR3
local v3Origin = actor:GetActorLocation()
local v3NewLocation = v3Origin + XVECTOR3(0, 0, 5)
actor:SetActorLocation(v3NewLocation)
而我们可以使用矩阵表达这次平移:
---@type XVECTOR3
local v3Origin = actor:GetActorLocation()
local m4 = XMATRIX4()
m4:Translate(0, 0, 5)
local v3NewLocation = m4 * v3Origin
actor:SetActorLocation(v3NewLocation)
可以看到,我们先获得了小明当前的位置向量,然后构造了一个向前走五米的矩阵。
使用矩阵和向量相乘,得到了一个新的位置向量,这个新的位置向量就是向前平移了五米之后的位置向量。
我们目前的小明Actor又回到了原点的位置,现在我们想控制小明往前方走5米。但是不同的是,小明站在原点的位置向右旋转了90度,小明的前方变成了X轴的正方向:
这时小明往前方走变成了:
---@type XVECTOR3
local v3Origin = actor:GetActorLocation()
local v3NewLocation = v3Origin + XVECTOR3(5, 0, 0)
actor:SetActorLocation(v3NewLocation)
可以看到,以小明的角度往前走这件事,需要加一个向量来完成。而这个向量的值,需要由当前小明的旋转状态来决定。我们想要一个无论小明旋转了多少次后,都想让小明不断地往前走。这时候使用小明当前的变换矩阵就可以很简单地做到这件事:
--获取当前的位置
---@type XVECTOR3
local v3Origin = actor:GetActorLocation()
--获取当前小明的矩阵
local m4Transform = actor:GetWorldTransform()
--把往前移动 转换为 以小明的状态往前移动
---@type XVECTOR3
local moveDelta = m4Transform * XVECTOR3(0, 0, 5)
local v3NewLocation = v3Origin + moveDelta
actor:SetActorLocation(v3NewLocation)
这个“把往前移动 转换为 以小明的状态往前移动”的操作,就是使用矩阵来表达变换的好处。
而这里的转换过程,使用到了矩阵乘法。
3. 矩阵的运算
3.1. 矩阵间相乘
对于矩阵乘法,矩阵乘法的规则如下所示:
$$
\left[ \begin{matrix} a11 & a12 & a13\ a21 & a22 & a23 \end{matrix} \right]
*
\left[ \begin{matrix} b11 & b12\ b21 & b22\ b31 & b32 \end{matrix} \right]
=
\left[ \begin{matrix} c11 & c12\ c21 & c22 \end{matrix} \right]
$$
当矩阵A的列数(column)等于矩阵B的行数(row)时,A与B可以相乘。
2x3的矩阵 不能 乘以4x5的矩阵
矩阵C的行数等于矩阵A的行数,C的列数等于B的列数。
2x3的矩阵 乘以 3x2的矩阵 得到 2x2的矩阵
新矩阵的每一个值的计算公式为:
$$
C{mn} = \sum{i=1}^NA(m,i)*B(i,n)
$$
即 新矩阵的第1行第2列的值 等于 第一个矩阵的第1行 点乘 第二个矩阵的第2列
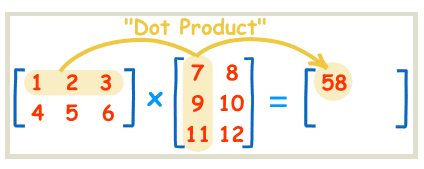
58 = 1 7 + 2 9 + 3 * 11
3.2. 矩阵和向量相乘
一个XMATRIX3类型的矩阵和一个XVECTOR3类型的向量相乘,会先把XVECTOR3隐式转换为一个1x3的矩阵:
举个例子,一个XVECTOR3(1.5, 2.5, 3.5) 会被转换为矩阵:
$$ \left[\begin{matrix} 1.5\ 2.5\ 3.5 \end{matrix}\right] $$
然后矩阵和向量相乘,其实还是矩阵之间的乘法运算。
3.3. 乘法规律
矩阵间的乘法是满足结合律的,但是不满足交换律:
$$ (A \cdot B) \cdot C = A \cdot (B \cdot C)
$$
$$ A \cdot B \cdot C \neq A \cdot C \cdot B
$$
这样我们可以通过矩阵的连乘来记录一系列的变换操作:
一个记录了先平移再旋转再平移的矩阵:
local v3Origin = XVECTOR3(0, 0, 5)
local t1 = XMATRIX4()
t1:Translate(0, 0, 5)
local r = XMATRIX4()
r:RotateAxis(XVECTOR3(0, 1, 0), math.pi * 0.5)
local t2 = XMATRIX4()
t2:Translate(0, 0, 5)
local m4 = t1 * r * t2
local vNewLocation = m4 * t1
print("vNewLocation: ", vNewLocation.x, vNewLocation.y, vNewLocation.z)
输出:
vNewLocation: 10 0 5
3.4. 矩阵的逆
矩阵间没有除法运算,但是可以通过求逆来得到某个矩阵完全相反的操作,之后乘以这个逆矩阵来进行一次相反的变换。
对于求逆操作,只有方阵(即NxN矩阵)才有逆矩阵。不过万幸的是,引擎提供的XMATRIX3和XMATRIX4都是方阵(分别是3x3和4x4的方阵)。
求逆的数学运算先按下不讲,引擎提供了求逆函数来快速求得逆矩阵:
m4:Inverse()
对于矩阵的逆的使用,上面有用到获取一个Actor的世界矩阵:
local m4 = actor:GetWorldTransform()
这个世界矩阵可以将世界坐标系下的向量 转换为 Actor坐标系下的向量:
--世界坐标系下的向量
local v3 = XVECTOR3(0, 0, 5)
--Actor坐标系下的向量
local nv3 = m4 * v3
而该矩阵的逆矩阵,正好可以做到相反的转换:
--Actor坐标系下的向量
local v3 = XVECTOR3(0, 0, 5)
m4:Inverse()
--世界坐标系下的向量
local nv3 = m4 * v3

